As part of its engagement with SASB’s human capital management project, Rights CoLab teamed up with the Data for Good Scholars (DfG) Program of Columbia University’s Data Science Institute to identify new relationships between labor-related human rights risks and financial materiality using natural language processing (NLP) and other machine learning data science methods.
In consultation with the project Expert Group and others with experience in AI and human rights, we identified two work streams to address previous gaps in data collection: what we came to call the “Addition Project” and the “Extension Project.” Each workstream examines a different criterion of SASB’s definition of financial materiality. The Addition Project examines the financial impact of corporate labor-related practices derived from news sources; the Extension Project examines investor interest through Form 10-Ks, proxy statements, earnings calls, etc. The report on the first phase of work describes the methodological decisions made to build text processing models, including the selection of keywords and phrases for machine learning, and of datasets for building the data model.
Isha Shah, Alexander Jermann, Anna Guerrero, Lawrence Lai, Jason Kao, Ryan Guo, and Archit Matta are the members of the DfG project team carrying out the work under the supervision of Dr. Vincent Dorie. Since the first DfG report in September 2020, the students have tested different approaches for each of the two work streams to identify the highest performing models that meet a high accuracy threshold. This update describes those efforts and lays out the next steps.
Workstream 1: The Addition Project
New Labor Rights Metrics
The Addition Project aims to identify relationships between labor rights metrics not currently in the SASB standard and financial impact across a broad range of SASB industry standards.
Our current methodology involves the following tasks:
- Collecting a corpus of news articles that contain mentions of either certain labor practices or financial risks that could be associated with them
- Observing the co-occurrence of labor-relevant corporate practices (e.g., “debt bondage,” “modern slavery,” etc.) and financially impactful outcomes (e.g., “lawsuits,” “strikes,” etc.)
The Expert Group defined the terms we used to retrieve articles for both relevant labor practices and financial risk. To test the viability of our methodology, the team started with a small sample of news articles from The New York Times that matched any of the defined risk and/or practice terms. The team found a co-occurrence relationship between risk and practice terms, which suggested this relationship might also exist on a larger sample of news articles. Thus we opted to scale the retrieval of news articles by using Contextual Web API,[1] an affordable subscription database that automatically collects articles from a plethora of news publishers. The team chose this API to reduce bias in the topics published or the language used, which is often introduced when using a single source. Contextual Web API seemed to offer a viable alternative to corporate news aggregators, which charge substantially more for access to their news articles. However, after reviewing preliminary results, the team determined that Contextual Web API led to inferior data, including duplicate news articles and untrustworthy sources. Because news article publication dates were inaccurate, we could not determine the number of duplicate articles, nor could we confirm how many of the total existing articles we had retrieved.
We adopted the alternative approach of selecting a group of publishers and retrieving news articles directly from each source. Our selection criteria were twofold: 1) the news publisher maintains API access so that we could programmatically retrieve news articles; and 2) the news publisher is an internationally recognized publication with broad geographic coverage. In addition to The New York Times, we added The Guardian, which is known for strong global reporting on human rights. We are planning to expand the corpus to The Financial Times and Reuters soon and are exploring how to gain access to local newspapers in high-risk contexts. SASB has provided us with a list of risk terms already reflected in the existing SASB Standard. We will use these terms to create an additional approach for identifying human rights–related corporate practices that co-occur with those risks.

In total, we retrieved 265,851 articles from The New York Times and 143,841 articles from The Guardian for the period 1 January 2008 to 1 January 2021. With this corpus of news articles, we used natural language processing, a subfield of machine learning, to align the articles. We then built co-occurrence tables to understand how practices and risks correlated in the articles. The matrix below shows the co-occurrence percentage of practice and risk terms on the corresponding intersection. For example, in news articles using the practice term “wage violation” (third row), the term “lawsuit” also appeared in 30% of them (third column, left yellow square). Each column and row on the matrix includes the singular and plural versions of the terms (e.g., we retrieved articles using “lawsuit” and “lawsuits”).
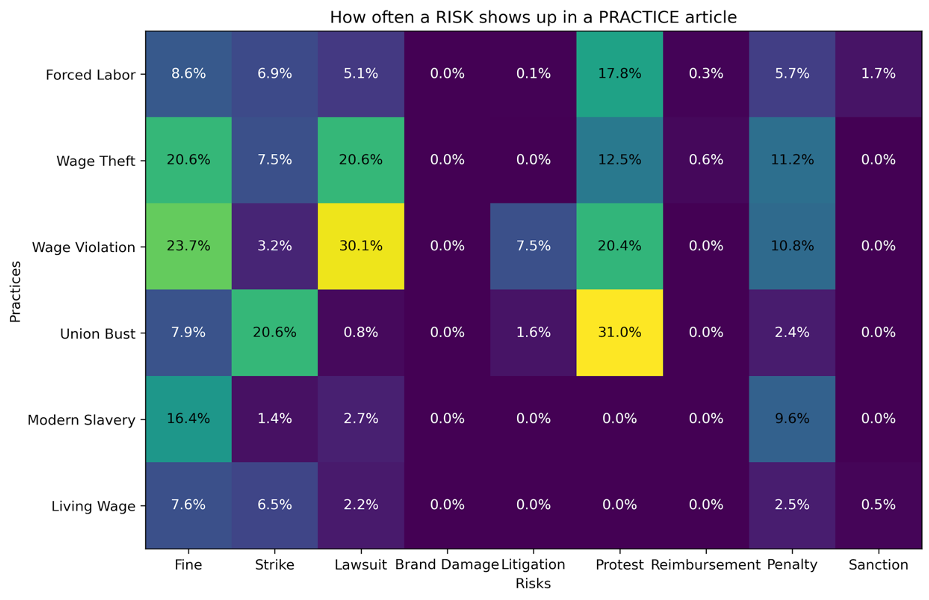
Table A: This table shows the preliminary percentages of co-occurrence of risk and practice terms in our New York Times article dataset. Here, we retrieved articles using only practice terms (e.g., forced labor, wage theft) and calculated the percentage of times a risk term (e.g., protest, lawsuit) co-occurred within that news article.
The second matrix is similar, with the key difference being that we retrieved articles using the risk terms. We assessed the co-occurrence using the same approach as the previous matrix. Looking at our new results, we observe that the intersection between “lawsuit” (third row) and “wage violation” (third column) is no longer 30%, as it was when we began with the practice term; rather, it is 0.1% now. These results stem from the fact that there are many more articles containing risk terms than practice terms. For example, searching The New York Times for “forced labor” returns 720 articles while “lawsuits” returns 29,454 articles.
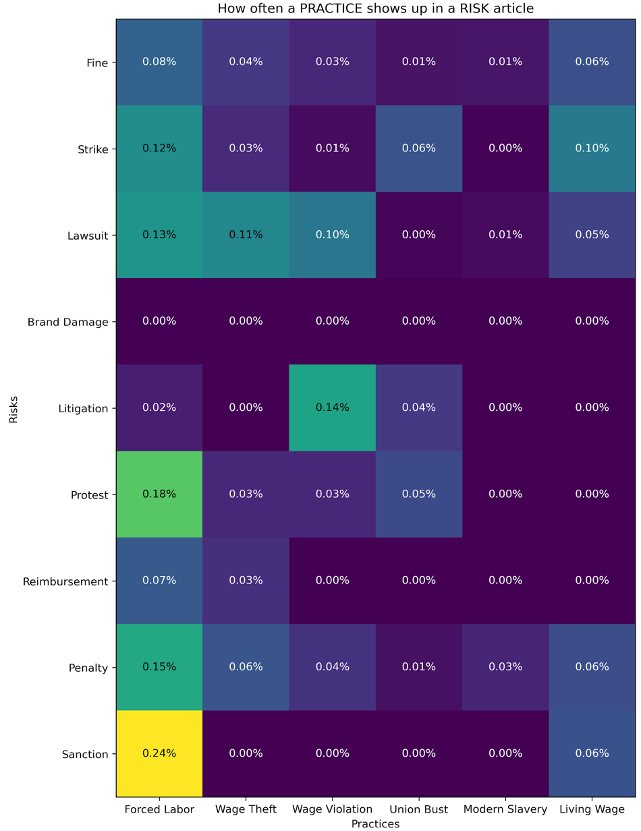
Table B: This table shows the preliminary co-occurrence percentages of risk and practice terms in our New York Times article dataset. We retrieved articles using risk terms (e.g., “protest,” “lawsuit”) and calculated the percentage of times a practice term (e.g., “forced labor,” “wage theft”) co-occurred in that same article.
To make these results more interpretable, we will combine both matrices, which we expect will clarify the association between the term pairs. Ultimately, we hope to make this matrix interactive so that our audience can more easily locate examples of news articles in which the given terms co-occur.
Currently, we are only retrieving the news article titles and their unique IDs since 1) the titles contain the most relevant information; 2) the full body text is not provided through the API for all news publishers; and 3) the co-occurrence analysis does not require full body text since the search retrieves articles if the keyword appears anywhere in the text even if it does not show us that text.[2] For example, if we search The New York Times for the term “wage violation,” we receive all the articles that contain that phrase anywhere in the text even though we can only retrieve the title.
We have also accessed the API of the Business & Human Rights Resource Centre (BHRRC). Since 2003, BHRRC has tracked the human rights policy and performance of over 10,000 companies across a broad range of NGO reports and English and foreign language news sources, both international and local. Their database is invaluable not only for providing more cases for analysis of co-occurrences, but also because all the items it hosts are related to corporate human rights impacts and therefore can inform our set of practice and risk terms. We are using the BHRRC API to build a labor rights–specific vocabulary for retrieving new articles not yet found with current search terms in The New York Times and The Guardian.
When retrieving news articles using only risk terms such as “protest,” or only practice terms such as “forced labor,” we get two separate sets of articles that overlap only if both articles contain both risk and practice terms. In conducting NLP, it is essential to understand the fundamental differences and biases of data sources in order to accurately interpret what they tell us. In the case of the BHRRC, we know that 100% of the articles retrieved using a risk term overlap with those using practice terms. In other words, all risk news articles or reports in the BHRRC are “practice articles,” meaning they are related to corporate practices.
On the other hand, not all items retrieved from the BHRRC API using a practice term also have a risk term. For example, if we search for the risk term “protest,” we can be confident that the results will provide articles about a corporate practice with human rights implications. But if we search BHRRC for the practice term “recruitment fee,” not all articles contain risk terms because some articles may be about a positive step a company took, for example, to eliminate the practice of recruitment fees. By contrast, for The New York Times the word “protest” might refer to a government protest unrelated to corporate practice. For the major international news sources, we do not know how many risk articles are also practice articles, but the risks are unlikely to be 100% related to corporate practices, unlike for the BHRRC.
In this way, both the major international newspapers and the BHRRC can help us answer different but equally useful questions. The New York Times allows us to ask, “How many times are articles that contain a company risk term, such as “protest” or “lawsuit,” related to a company’s labor practices?” On the other hand, the BHRRC API allows us to ask, “For what sectors are news articles about the presence or absence of potentially harmful corporate labor practices related to a corporate risk or the mitigation of that risk?”
Next Steps for the Addition Project
Over the coming months, the Addition team will work on three main tasks: 1) developing a more robust co-occurrence matrix; 2) building an industry classifier for news articles; and 3) exploring the financial materiality of news articles through an event study.
After consulting with Factset’s TruValue Labs data scientists, Ryan Roser and Yang Ruan, we decided to focus on ensuring the robustness of the matrix in several ways: 1) retrieving news articles from more sources (e.g., The Financial Times, BHRRC, Reuters, etc.); 2) aggregating results from different news sources; 3) combining the two matrices into a single matrix; and 4) providing examples of news articles where risk and practice co-occur.
To highlight the statistical significance, we will also develop a model to predict whether a news article from the risk and/or practice dataset is financially material. The prediction is worded as follows: “Is the labor rights practice term contained within the text body of an article with a risk term financially material, yes or no?” To evaluate the accuracy and quality of the prediction, we will use news articles already determined to show financial materiality. If our prediction is often right, we can establish that the relationship is statistically significant.
As an intermediate step, we will use SASB’s industry classification on news articles to design industry-specific labor rights metrics. Here we will use a technique from a subfield of natural language processing called “named entity recognition” (NER). For this step we need full-body text of news articles, which are available for a subset of publishers.
Lastly, the Addition team is exploring the possibility of providing evidence for financial materiality through an event study. Using the publication date of a news article, the team seeks to measure the financial impact of an event (i.e., co-occurrence of a risk and practice term in an article) on a given company. Instead of using stock price to assess financial impact, the SASB research team has advised us to use revenue or earnings as more reliable indicators.
Workstream 2: The Extension Project
The Extension Project aims to expand the Human Capital Management (HCM) topics and metrics, which currently apply to some SASB industry standards, to a broader range of industries by demonstrating investor interest in the topics or metrics for those industries not currently containing that indicator. In this way, we are seeking to fill in the white spaces on the SASB Materiality Map shown below.
We began with two strategies: supervised learning on 10-Ks and unsupervised learning on proxy statements. Our focus is primarily on two SASB General Issue Categories (GICs): Labor Practices and Supply Chain Management.[3] Through pre-processing steps on the training data, testing different classification methods, and tuning parameters, we have worked to refine the model. Below we describe this process for each strategy.
Supervised Learning on Form 10-Ks
SASB determines materiality through evidence of investor interest and financial impact from a variety of sources. Our classifier, once better developed, will be applied to several data sources, including 10-Ks and proxy statements, which we prioritized in building the classifier. As well, no action requests, proxy advice, 10-Qs, quarterly earnings calls, and sell-side reports are also used.
SASB shared with us its labeled data for 10-Ks for its HCM and Business Models and Innovation dimensions to train the classifier. Form 10-Ks offer a good starting point for the following reasons:
- 10-Ks are all in a single format on EDGAR, and it is easy to retrieve a wide sample of filings, including across industries and going back in time.
- SASB itself deems 10-Ks to be a highly valuable measure of investor interest; therefore, SASB is likely to be persuaded by this evidence.[4]
To identify gaps in SASB’s materiality map, we tested two approaches using this dataset. First, we built an industry-agnostic classifier to train on a dataset provided by SASB. The dataset labeled each paragraph in the forms as relevant or not relevant to the HCM dimension and the GICs within it. Then it applied the classifier to new 10-Ks and other datasets, thus vastly expanding available data across industries. Second, we trained a convolutional neural net[5] on the labeled dataset and then used transfer learning to apply the model to proxy statements to identify which classifications arise. The industry-agnostic classifier was successful and we will continue to refine it. The convolutional neural net was not successful, so we will retire it.[6] Our experience with the more successful approach is outlined below.
Industry-Agnostic Classifier
We built an industry-agnostic classifier to sort paragraphs from the SASB labeled dataset into those relevant to the HCM dimension and to the Supply Chain Management GIC. We tested multiple models and selected the highest performer, a multiclass XGBoost classifier, which offers about 81% predicting accuracy.[7]
The classifier will enable us to compare the frequency of these topics in the 10-K corpus for industries without recommended disclosures to those industries with them. The information can then be used to make the case for an extension of the standard to industries relevant to each topic. We ran various iterations of the model to identify problems with the classifier and steadily refine it. This process will continue with the goal of creating a model that performs reliably on both the original SASB labeled dataset (the training dataset) as well as a larger corpus of 10-Ks. Ultimately, the model will analyze firms in all industries, including those with and without a human capital or supply chain disclosure standard.
Refining the Model
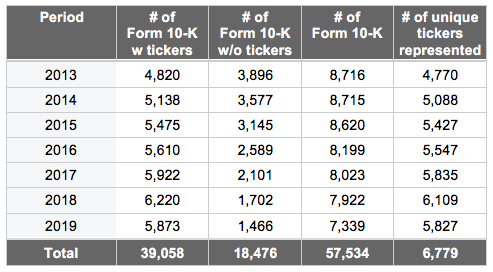
Next, we tested the XGBoost model on a more recent, more varied set of 10-Ks than those from SASB. The dataset from SASB contained 10-Ks collected prior to 2018 and were limited to only those industries in which the current standards are deemed material. We downloaded and extracted textual data from over 57,000 10-Ks filed between 2013 Q1 and 2019 Q3 from SEC’s Electronic Data Gathering, Analysis, and Retrieval (EDGAR) system. The following table summarizes the data extraction results.
To get our textual data ready for machine learning tasks, we pre-processed the texts into disclosure paragraphs and then into vectors[8] based on the same word embeddings used to train the XGBoost model.
We performed an initial evaluation of the XGBoost model by classifying all disclosures from the new 10-K corpus based on their relevance to HCM. Next, we reviewed the results using the Fall 2020 model. The XGBoost model performed fairly well in classifying disclosures not relevant to HCM (i.e., true negatives), but did not perform as well in classifying disclosures relevant to HCM (i.e., true positives). More specifically, we observed that,
- False positives (i.e., paragraphs incorrectly classified as irrelevant) consisted of the following: questionnaires at the beginning of Form 10-K, boilerplate language (e.g., with the word “registrant”), and other disclosures related to business practices, risks, general interest rates, investments, insurance coverage, dividend policy, debts, biographies, etc.
- False negatives (i.e., paragraphs incorrectly classified as relevant) consisted of the following: disclosures related to employee compensation (e.g., stock options), retirement plans (e.g., pension and savings plans), and labor-related items (e.g., strikes, contract violations).
From the initial evaluation, we learned that we could improve the performance of the existing XGBoost model by modifying our data pre-processing approach and/or using additional training data. To clean our corpus data, we eliminated boilerplate paragraphs and expanded the vectorization to include bigrams (word pairs). We also explored other vectorization approaches (e.g., token counts, TF-IDF, etc.) and other classifiers (e.g., logistic regression, SVC).
After refining the pre-processing steps, we again applied the classifier to the cleaned corpus, and extracted 1,000 disclosures to review manually. After we verify the accuracy of the labels on these records, we will add them to the SASB labeled dataset in order to train the multiclass classifier again, this time on both the original labeled 10-K paragraphs and those from the new corpus.
Visualizing the Classification Results on Disclosure Activities
The following are preliminary visualizations to help benchmark the relevant disclosure activities by industries that do not currently have an HCM topic (“White Space Industries”) against the relevant disclosure activities by industries where the topic is applicable (“Benchmark Industries”) from 2013 to 2019. These results are generated from a Linear SVC, one of the other models we trialed, which yielded slightly better accuracy than the existing multiclass XGBoost model. For this model, we followed the approach of 1) vectorizing our disclosure paragraphs using term frequency–inverse document frequency (“tf-idf”), and 2) training our model using linear support vector classification (LinearSVC). We will produce the same visualization for the final model chosen.
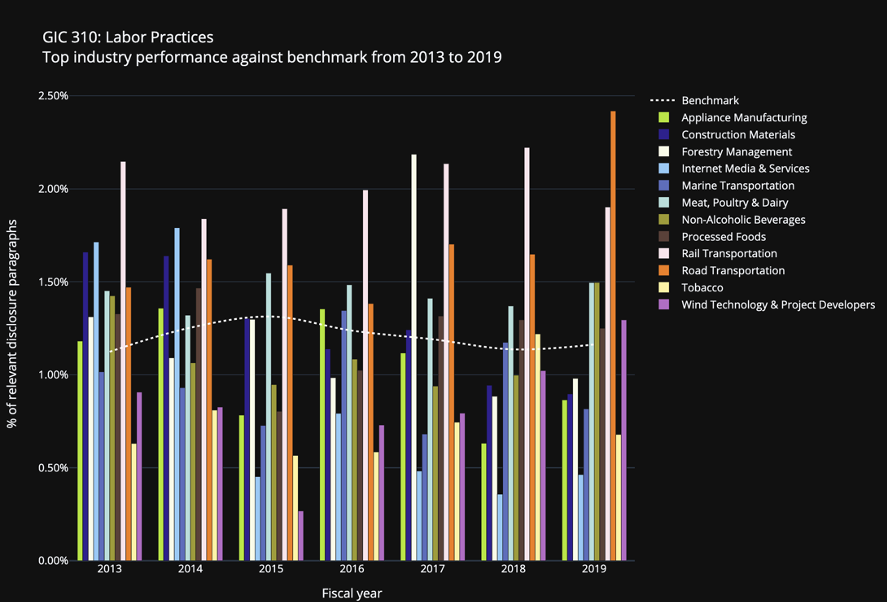
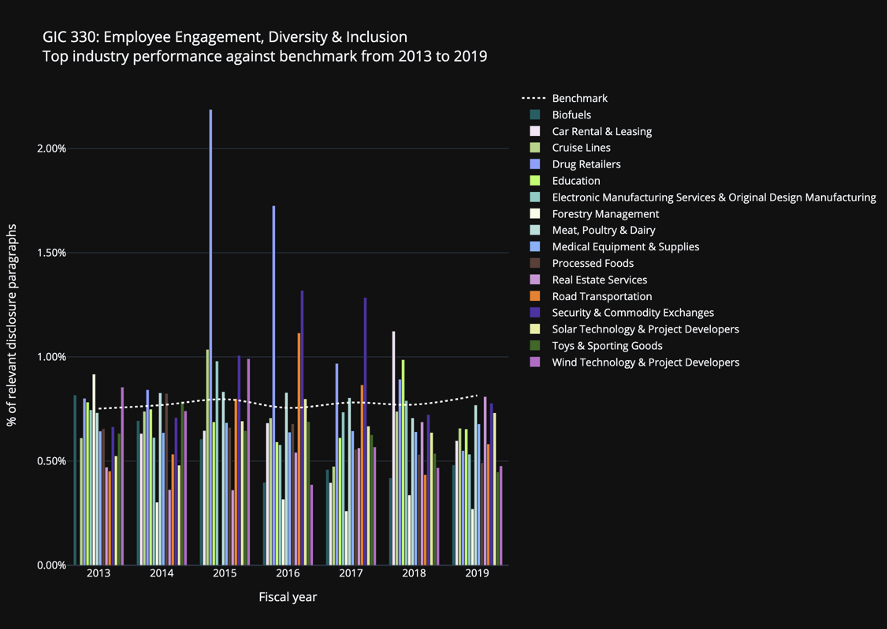
The bars represent the relevant disclosure activities for certain White Space Industries by year as evaluated against the benchmark — or the relevant disclosure activities for Benchmark Industries by year, represented by the white dotted line. Any White Space Industries that had more relevant disclosure activities than the Benchmark Industries are of interest because they indicate both improvement opportunities to our classification models and industries in which a specific HCM standard may potentially be applicable.
For this preliminary visualization, we measured the relevant disclosure activities for all companies within both White Space and Benchmark Industries based on their respective percentage of disclosure paragraphs within the 10-Ks deemed relevant to the specific HCM standard. For example, if Company A has one paragraph relevant to labor practices out of 100 paragraphs within its Form 10-K for 2019, then its percentage of relevant disclosure paragraphs for labor practices is 1% for 2019. At the industry level, we used the median of the percentage of relevant disclosure paragraphs across all companies within an industry as the aggregated measure.
Unsupervised Learning on Proxy Statements
Proxy statements represent a corpus of data that can provide a valuable indicator of investor interest, even as the corpus is biased towards progressive investors who engage in shareholder advocacy to encourage companies to adopt sustainability measures.
We used unsupervised clustering[9] on proxy statements downloaded from EDGAR for the period 2010 Q1 to 2020 Q1 to identify only those sections relevant to SASB’s Labor Practices and Supply Chain Management GICs in order to reduce the volume of documents requiring human analysis. Once classified as relevant, these statements can be further sorted into specific topics, using either further unsupervised clustering or a transfer learning method, where SASB 10-K labeled data is applied to proxy statements. Our aims are to:
- Identify sections of proxy statements relevant to the SASB standards by clustering paragraphs of proxy statements to separate irrelevant from relevant paragraphs.
- Find potential new categories of materiality by clustering relevant paragraphs and mapping clusters to SASB’s HCM dimension and Supply Chain Management GIC topic areas. For clusters outside of these areas, we considered if they could potentially represent new topics.
- Provide a launching point for labeling proxy statements, so that SASB can apply a broader range of techniques to parse data by creating approximate category labels using clusters.
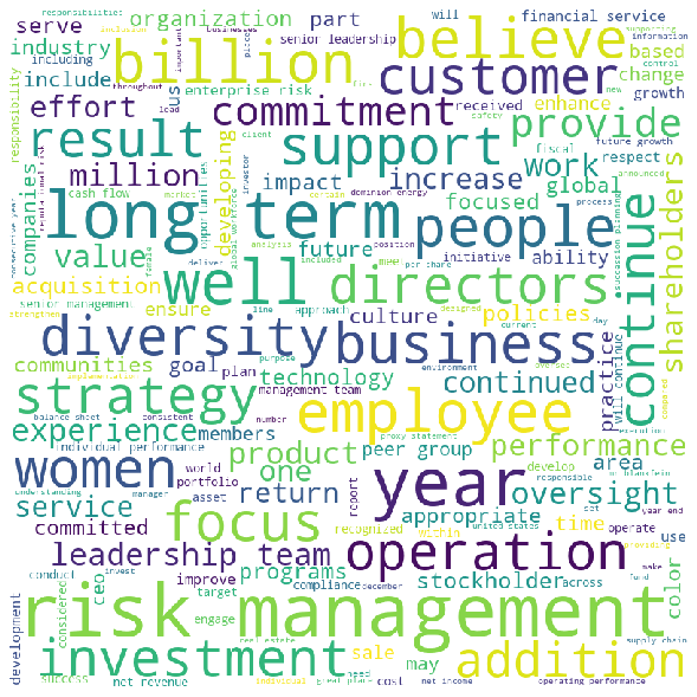
We iteratively clustered the paragraphs, removing the obviously irrelevant ones. By the fourth round of refining clusters, irrelevant paragraphs had been largely removed. The remaining individual clusters each suggested a separate area of materiality. Below is an example word cloud for Cluster 6, where the words “women,” “diversity,” “employee,” and “work” are shown.
We are working to refine pre-processing, implement labeling algorithms, and implement weak supervision using Snorkel, a system that manages training data. This involves two main steps:
- Refining preprocessing by removing additional stop words — or words without meaning. Within the proxy statements, more definitive clusters can be produced by removing stop words so that the top words in the individual clusters will help identify areas of corresponding materiality. For instance, the word “stockholder” is a commonly used term in proxy statements. By itself, it has little to do with materiality. By removing all instances of this word, the clustering algorithm will not consider it as a criterion for grouping.
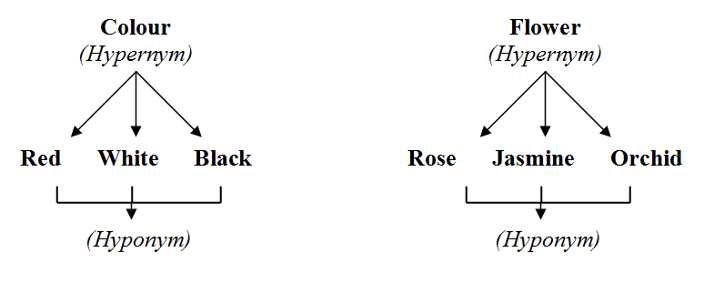
- Labeling algorithms sourced from WordNet API using hypernyms — or words whose meaning includes the meanings of other words. The most relevant keywords are extracted from the clusters so that a hypernym can be found, thereby producing a cluster label such as “health care” or “diversity.” WordNet might also be promising as a tool to perform this labeling.
Weak Supervision Using Snorkel
We attempted to use weak supervision — a model that uses less precise data sources than a labeled dataset — to begin labeling clusters to create a training dataset that could eventually be an input to the classifier. The Snorkel algorithm is one approach, but since it requires much trial and error, it will take some time to yield significant results.
Next Steps for the Extension Project
Currently, our classifier for Form 10-Ks can identify paragraphs that contain HCM-related disclosures with close to 80% accuracy according to a partially labeled dataset. The clustering performed on the proxy statements is still in the process of generating tentative labels. For both approaches, we will hand-label additional forms to further train our classifier to provide an acceptable level of accuracy for robust analysis.
Once the classifier can reliably detect labor-related disclosures in 10-Ks, we will be able to determine their relative frequency in different industries, including those for which the topic was not deemed material in current SASB standards. We will then apply the refined classifier to new Form 10-Ks and label each paragraph as containing or not containing any relevant disclosures relevant to labor practices, employee health and safety, and employee engagement, diversity, and inclusion. We will then analyze the share of 10-Ks in each industry that contains paragraphs relevant to each GIC. The same procedure will be repeated with SASB’s labeled data set for Supply Chain Management and Business Model Resilience GICs of the Business Models and Innovation Dimension.
Additionally, the team will continue to refine an unsupervised learning tool to label proxy statement paragraphs as either relevant or not relevant to labor, and then sort them into those same GICs as used for the 10-Ks.
Conclusion
Once these models are further refined for accuracy, they can be applied to any of the SASB GICs. In addition, we see scope for integrating the Addition Project with the Extension Project. For example, where the sample size is large enough, we can structure the Addition Project matrix by industry to match the chart of the paragraph mentions of the Extension Project once we have created it for Supply Chains. For each of those industries we will be able to see what the most prominent risks are. Our next report will address these results.
[1] API stands for Application Programming Interface.
[2] We have verified this by visiting the news article website.
[3] Supervised learning means that the model learns by example on a labeled dataset that has an answer key to evaluate accuracy, while unsupervised learning means that a model tries to make sense of unlabeled data by extracting patterns on its own. Learn more.
[4] In our previous report we asserted that 10-Ks are also “a strong indicator of financial impact/risk since they represent the company’s own judgement of risk.” We are retracting this statement. Form 10-Ks can reflect financial impact in the sense that companies are advised to report potential risk and they may have impact. However, as 10-K disclosure is designed to inform investors of risks that the issuer thinks investors would find material, more often than not companies are reporting what they believe investors are interested in. To the extent that investor interest in a topic impacts investor’ decision-making, that topic can be seen as financially material. See: Top 10 Practice Tips by Experts: Risk Factors 2 (2017).
[5] A convolutional neural net is an algorithm that assigns importance to an input image and is then able to differentiate one from another. Learn more.
[6] While this approach did not perform well, if time permits, the team may try again using autoencoders to reduce the dimensionality of the labeled dataset.
[7] While this level of accuracy is sufficient to move forward with the corpus of new 10-Ks, we will continue to attempt further parameter optimization to improve accuracy.
[8] A vector is a representation of a paragraph that can be used by machine learning techniques to assess similarity.
[9] Unsupervised clustering maps relevant paragraphs and clusters to two of SASB’s GICs: Human Capital Management and Supply Chain Management. If clusters contain content outside these two GICs, we consider whether they might represent new GICs.
Photo by Maria Teneva on Unsplash
